今回の題材は関数論講義(金子晃)の第1章から。この本、第1章から目から鱗が落ちる。
対数関数の定義
対数関数は指数関数の逆関数として定義されることが多い。指数関数はオイラーの公式を使って定義されることも多いが、冪級数を使った定義 \( \displaystyle e^z = \sum_{n=0}^\infty \frac{x^n}{n!} \) の方が理論を構築しやすいように思う。複素関数としての指数関数は多対1なので、逆関数である対数関数は多価関数になり、\( \log z = \log |z| + i \, \arg (z) \) で表される。\( \arg (z) \) は \( 2n\pi \) の差があっても同じ \( z \) を表すため多価関数になる。
逆三角関数
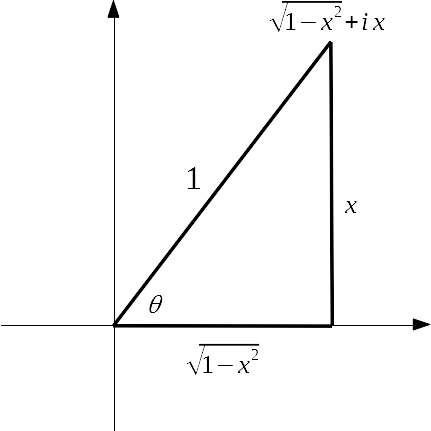
逆三角関数は実関数としてもすでに多価関数なので、とうぜん複素関数としても多価関数である。逆三角関数は対数関数で表され、多価性は対数関数に起因するというのが驚きだった。\( \sin \theta = x \) とすると、\( \theta = \mathrm{Arcsin} \,x \) である。平面を複素平面と見なすと、\( \displaystyle \theta = \arg \left( \sqrt{1-x^2} + i \, x \right) \) となる。\( \log \left( \sqrt{1-x^2} + i \, x \right) \) の対数を計算すると
\( \begin{eqnarray}
\log \left( \sqrt{1-x^2} + i \, x \right)
&=& \log 1 + i \,\arg \left( \sqrt{1-x^2} + i \, x \right) \\
&=& i \,\arg \left( \sqrt{1-x^2} + i \, x \right)
\end{eqnarray}\)
となり、\( \mathrm{Arcsin} \,x \) は \( -i\,\log \left( \sqrt{1-x^2} + i \, x \right) \) と対数を使って表された。\( \mathrm{Arccos} \,x \) や \( \mathrm{Arctan} \,x \) も対数を使って表現できる。
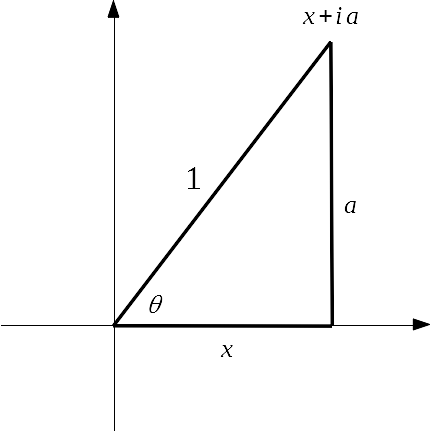
Arctan の性質
メインテーマの準備として \( \mathrm{Arctan} \) の性質を議論しておこう。底辺の長さが \(x\)、高さが \(a\) の直角三角形を考えると、\( \displaystyle \arg (x+ia) = \mathrm{Arctan} \left( \frac{a}{x} \right) \) と分かる。\( \log ( x \pm ia ) \) を計算しよう。
\( \begin{equation} \log ( x \pm ia ) = \log \left( \sqrt{x^2+a^2} \right) \pm i \,\mathrm{Arctan} \left( \frac{a}{x} \right) \tag{1}
\end{equation} \)
\( x>0 \) に対して、次の公式を証明しておこう。
\( \begin{equation}
\mathrm{Arctan} \,x + \mathrm{Arctan} \frac{1}{x} = \frac{\pi}{2} \tag{2}
\end{equation} \)
これは直角三角形を使って初等的に証明できるが、解析的に証明してみよう。左辺を \(f(x)\) と置くと
\(\displaystyle
f'(x) = \frac{1}{x^2+1} -\frac{1}{x^2}\cdot\frac{1}{1+\frac{1}{x^2}} = 0
\)
\(\displaystyle f(1) = \frac{\pi}{4} + \frac{\pi}{4} = \frac{\pi}{2} \) だから \( \displaystyle f(x) = \frac{\pi}{2} \) を得る。
積分への応用例
\(a>0\) として、2つの積分を見比べてみよう。
\( \begin{eqnarray}
\int \frac{1}{x^2-a^2} \, dx &=&
\frac{1}{2a}\left( \log (x-a) – \log (x+a) \right) +C \tag{3} \\[3mm]
\int \frac{1}{x^2+a^2} \, dx &=&
\frac{1}{a} \mathrm{Arctan} \,\frac{x}{a} +C \tag{4}
\end{eqnarray}\)
結果は大きく違うように見えるが、(3) で \(a\) の代わりに \(ia\) を入れると (4) が得られてしまうという。(3) 右辺の \(a\) を \(ia\) で置き換えて、(1) を使って計算する。
\( \displaystyle
\frac{1}{2ia}\left( \log (x-ia) – \log (x+ia) \right)
= -\frac{1}{a}\mathrm{Arctan} \left( \frac{a}{x} \right)
\)
(2) を用いると
\( \begin{eqnarray}
&=& – \frac{1}{a}\left( \frac{\pi}{2} -\mathrm{Arctan} \left( \frac{x}{a} \right) \right) \\[3mm]
&=& \frac{1}{a}\mathrm{Arctan} \left( \frac{x}{a} \right) \,-\, \frac{\pi}{2a}
\end{eqnarray} \)
第2項の定数部分は積分定数に含められるので、(4) の右辺に等しい。
残された疑問
\(x>0\) に対して、\( \displaystyle \mathrm{Arctan} \,x + \mathrm{Arctan} \frac{1}{x} = \frac{\pi}{2} \) を示した。\(x<0\) の場合を考えてみると \( \displaystyle \mathrm{Arctan} \,x + \mathrm{Arctan} \frac{1}{x} = f(-1) =-\frac{\pi}{2} \) となる。当初、\(x=0\) で不連続であるから不思議に思わなかったが、複素変数にして接続できるならば関数等式に違いがあることは不可解に思える。今のところ理由がはっきりしないので、とりあえず書き留めておく。単純な勘違いで、この記述が削除できることを期待する。
